DEFINICIÓN Y NECESIDAD DE LAS CURVAS DE NIVEL
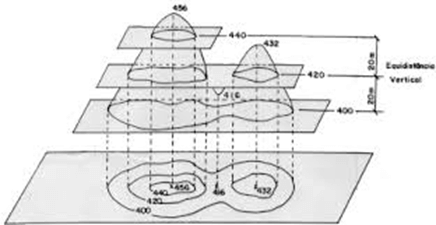
Sin entrar en definiciones mas profundas diremos que una curva de nivel es una línea que representa una elevación constante. Los mas puristas dirán que es una línea que representa un valor constante de potencial gravitatorio pero para no complicarnos lo vamos a mantener simple.
La verdadera utilidad de las curvas de nivel reside en que hasta hace no mucho las representaciones de información se realizaban exclusivamente en papel. Por tanto, la utilidad de las curvas de nivel es que nos ayudan a representar fenómenos tridimensionales de forma bidimensional.
PROPIEDADES DE LAS CURVAS DE NIVEL
1. Las curvas de nivel deben cerrarse sobre si mismas, ya sea dentro o fuera del mapa.
Esta es una de las reglas mas dificiles de comprender pero para entenderla veamos la siguiente imagen:
En principio parece que las curvas de nivel no se cierran, pero si ampliamos un poco mas la vista veremos que algunas curvas se comienzan a cerrar, y las que quedan abiertas tarde o temprano se terminarán cerrando si ampliamos cada vez mas la vista.
2. La distancia entre las curvas de nivel indica la magnitud de la pendiente. Un amplio espaciamiento indica una pendiente suave, por el contrario un espaciamiento estrecho indica una pendiente muy fuerte, un espaciamiento uniforme significa pendiente constante
Como se observa en la figura siguiente en la esquina superior derecha de la imagen en planta se observa que las curvas de nivel están mas juntas que hacia la izquierda abajo, cosa que se refleja en el perfil, a donde se agrupan mas es mas empinado que donde no.
3. Las curvas de nivel con forma irregular indican un terreno accidentado. Líneas con curvatura mas regular indican pendientes y cambios mas graduales.
Vean como en la figura las curvas de nivel no son tan quebradas como en la imagen anterior, eso produce que en el perfil se reflejen pendientes no solo constantes (congruentes con la regla anterior) si no que tambien casi perfectas.
4. Las curvas concéntricas y cerradas cuya elevación va aumentando de afuera hacia adentro representan montañas o elevaciones en el terreno. uLas curvas concéntricas y cerradas cuya elevación va disminuyendo de afuera hacia adentro representan depresiones en el terreno.
Esta es una de las propiedades mas fáciles de seguir, vean como en la imágen siguiente se observan dos zonas de curvas concéntricas que al ver el perfil corresponden a una montaña y a un agujero.
5. Las curvas de nivel en fenómenos lineales (calles, ríos, líneas férreas, canales, etc.) presentan por lo general separación constante y tienen formas de “U” o de “V” en función de la forma de la obra. En calles las “V” apuntan en el sentido de disminución de elevaciones . En ríos las “V” apuntan en sentido contrario a la disminución de elevaciones
¿De que depende que las curvas en calles tengan forma de «U» o de «V»? Pues básicamente de que si las calles tienen doble bombeo o no. Veanlo en los siguientes ejemplos, como se ven las curvas de nivel en la calle y como es la sección transversal de la calle.
6. Las curvas de nivel son perpendiculares a las líneas de máxima pendiente
Esta es una de las propiedades que mas me gusta porque pone en escena la aplicación práctica del Álgebra vectorial, y la Geometría Descriptiva.
En la calle con doble bombeo anterior se ve que a lo largo de la calle las elevaciones van disminuyendo, pero tambien disminuyen hacia los lados para una sección transversal de la calle, por lo que una gota de agua irá hacia abajo a lo largo de la calle pero tambien hacia un lado y aplicando la suma vectorial se observa que realmente irá en el sentido de la línea roja que ademas es perpendicular a la curva de nivel.
7. Dos curva de nivel que representan diferente nivel jamás se tocan o se cruzan, salvo en caso de taludes verticales, muros o paredes. En los casos anteriores las curvas solamente coinciden en planta pero nunca se cruzan espacialmente.
Si una curva de nivel representa la elevación de un punto X-Y a través de una línea que dos curvas de nivel pasen por un punto representaría que ese punto tiene dos elevaciones y eso solo es posible en taludes verticales y paredes.
Vean la siguiente imagen, la diferencia de elevaciones entre la cancha de BKB y el área de juego de niños es de 4 metros (se puede ver porque aparecen elevaciones puntuales o viendo las elevaciones de las curvas de nivel)
Vean como las curvas de nivel de repente se agrupan comenzando la cancha, eso se debe a que entre la cancha y el área de juegos hay un muro de retención de 4 metros y por eso las curvas de nivel se juntan ahí.