Como solemos decir siempre una variable espacial permite el análisis de numerosos fenómenos naturales vinculados a una determinada ubicación específica. Ya en la entrada pasada hablábamos del objetivo de la Geoestadística: la necesidad de inferir cosas globales con base a una información puntual y muestral. La manera de inferir estos valores desconocidos con base en los datos puntuales muestrales conocidos es lo que se define como interpolación y para hacerlo disponemos de muchos algoritmos.
Los diferentes métodos de interpolación, sin embargo, puede presentar variaciones en el resultado que dependerán de:
- Las características de la variable
- La dependencia espacial entre las variables
- La modelación de las variables
- La distribución de los datos
- La forma en que fueron medidos los datos
- La variabilidad
- La elección del modelo de interpolación
Clasificación de los métodos de interpolación
Los métodos de interpolación no son exclusivos de la Geomática por eso antes de introducirnos en los que competen y son aplicables a nuestra área vamos a clasificarlos.
Por técnicas de interpolación
- Determinísticos: Son métodos de interpolación que ajustan a funciones matemáticas de forma precisa y por tanto el objetivo será encontrar los parámetros que definen esa función matemática.
- Geoestadísticos: Son métodos de interpolación basados en datos con estructura espacial, son modelos estocásticos es decir que son difíciles de representan con una función matemática.
Por la cantidad de datos que intervienen
- Locales: Operan en una vecindad, es decir, alrededor de la zona de interpolación. Así, el resultado de interpolación global es la unión de varias interpolaciones zonales.
- Globales: Realizan las estimaciones sobre todos los datos disponibles a la vez
En función del valor obtenido
- Exactos: Son los métodos cuyo resultado predicho es idéntico al valor medido y por tanto generan alto grado de certeza
- Aproximados: No predicen el mismo valor medido y por tanto la diferencia entre el valor medido y el predicho determina la calidad de la interpolación.
En función de la dimension del dato interpolado
- Puntuales: El valor interpolado es un punto
- Superficiales: El resultado de la interpolación es un área
Métodos mas conocidos de interpolación en Geomática
Con base en la clasificación anterior, ahora hablemos de los dos métodos más conocidos incluso por los que apenas van introduciéndose en área.
Polígonos de Thiessen y Voronoi
El método de interpolación por polígonos de Thiessen y Voronoi es un método de carácter local puntual con método de interpolación exacto.
Es un método muy utilizado principalmente en variables de tipo cualitativo, se basa en considerar que los puntos de una zona coinciden con el valor medido más próximo y generan, como consecuencia, zonas de influencia siendo el resultado la unión de polígonos que generan distintas zonas temáticas.

Los polígonos de Thiessen permiten generar resultados muy interesantes como este mapa que redibuja las fronteras de los países en función de la capital que más cerca este de una coordenada especifica.
Métodos de triangulación
Al contrario de los métodos de poligonación estos métodos generan una malla de triángulos irregulares (TIN) cuyos vértices son los puntos medidos y por tanto es un método local puntual exacto. Tiene la desventaja de que no puede predecir cimas o depresiones locales si no hay datos medidos en ellos.

Métodos de interpolación por triangulación
A lo largo del tiempo han surgido diferentes métodos de interpolación por triangulación tratando de encontrar la forma más eficiente, principalmente desde el punto de vista computacional, para realizar la interpolación. Entre los métodos principales podemos mencionar:
- Mediante diagonales: Cuyo objetivo es la búsqueda de diagonales más cortas posibles que no se intercepten, sin embargo es un proceso muy lento.
- De Garey: Descompone polígonos por lo que también es un proceso muy lento si tomamos en cuenta la cantidad de información que se maneja en Geomática.
- Radial: Establece relaciones entre un punto central y sus vecinos, el problema es que produce triángulos no deseados.

- Triangulación de Delaunay:
Es uno de los métodos más conocidos por ser computacionalmente muy eficiente.
El principio de triangulación consiste en generar circunferencias circunscritas en triángulos donde no hay ningún otro punto dentro de ella. Este método genera un tipo de triangulación única independientemente del punto por el que se comience

En nuestra próxima entrada vamos a hablar en detalle de un método de interpolación más avanzado que es el de Kriging y de cómo es que este método interpola.
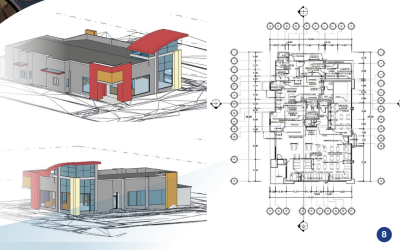
- Levantamiento arquitectónico tradicional con apoyo de vuelo de dron para generación de planos arquitectónicos y modelado BIM en Wendys.
- Control de verticalidad Ventus
- Levantamiento Topográfico con Fotogrametría con Dron en Zurita
- Levantamiento Topográfico en la zona del Monumento a la Reconciliación e integración del Bulevar Monseñor Romero con Avenida Jerusalén
- Consultoría del desarrollo de mapas georreferenciados para la mejora de la gestión de iluminación pública, recolección de residuos sólidos y mercados en algunos municipios seleccionados.